Variational bicomplex
It is a double complex defined in order to formalize Classical Field Theory, specifically Lagrangian field theory.
Consider the infinite jet bundle $J^{\infty}(E)$. We have that the Cartan distribution, or its dual expression the contact ideal, let us decompose
$$ \Omega^{p}\left(J^{\infty}(E)\right)=\bigoplus_{r+s=p} \Omega^{r, s}\left(J^{\infty}(E)\right) $$where $\omega\in \Omega^{r, s}\left(J^{\infty}(E)\right)$ if it is the sum of terms of the form
$$ f[u] d x^{i_{1}} \wedge \cdots \wedge d x^{i_{r}} \wedge \theta_{J_{1}}^{\alpha_{1}} \wedge \cdots \wedge \theta_{J_{s}}^{\alpha_{s}} $$with $\theta_I^{\alpha}$ the contact forms (see Anderson_1992).
$$ d: \Omega^{p}\left(J^{\infty}(E)\right) \rightarrow \Omega^{p+1}\left(J^{\infty}(E)\right) $$splits
$$ d=d_H+d_V $$where
$$ \begin{array}{l} d_{H}: \Omega^{r, s}\left(J^{\infty}(E)\right) \rightarrow \Omega^{r+1, s}\left(J^{\infty}(E)\right) \\ d_{V}: \Omega^{r, s}\left(J^{\infty}(E)\right) \rightarrow \Omega^{r, s+1}\left(J^{\infty}(E)\right) \end{array} $$Since $d^2=0$ and the decomposition is a direct sum we have that
$$ d_H^2=0 $$ $$ d_H d_V=-d_v d_H $$ $$ d_V^2=0 $$The double complex $\left(\Omega^{*, *}\left(J^{\infty}(E)\right), d_{H}, d_{V}\right)$ is called the variational bicomplex.
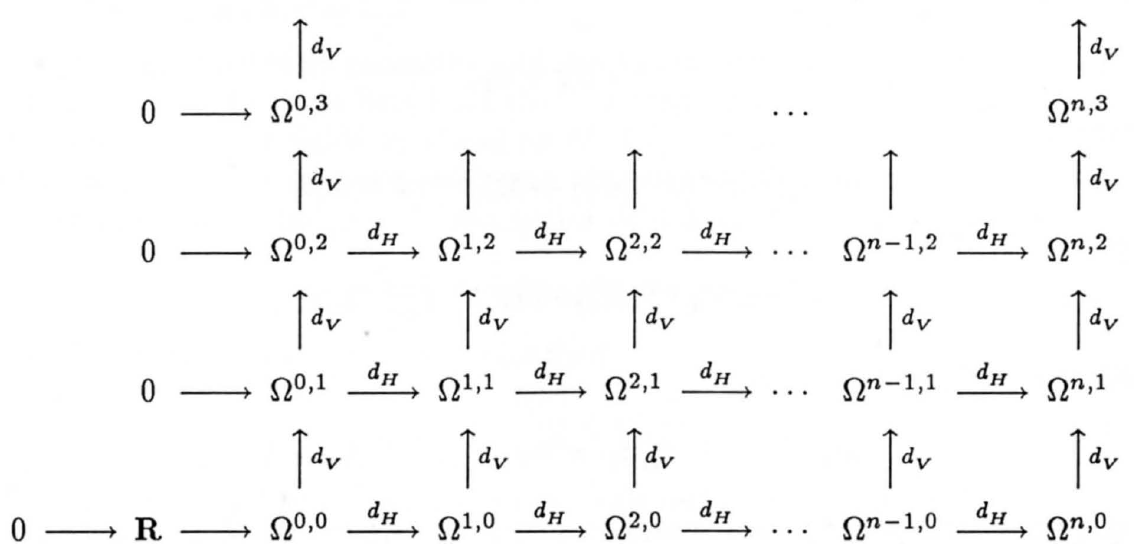
A form $\lambda\in \Omega^{n,0}$ is a Lagrangian for a variational problem.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: